The logic behind the standard kmeans is the Lloyd's algorithm the steps of which are as follows.Step 1 is to randomly initialize k distinct datapoints as centriods.
Step 2 iterate over each datapoint and assign them to the cluster with the centroid that has nearest euclidean distance to the point.
Step 3 update the centroids by setting them equal to the mean of all points in the relative cluster.
However, due to random initialization of the first centroids the k-means algorithm does not necessarily converge to optimal results.
In order to decrease the sensitivity of the k-means algorithm to random initialization, multiple techniques have been developed.
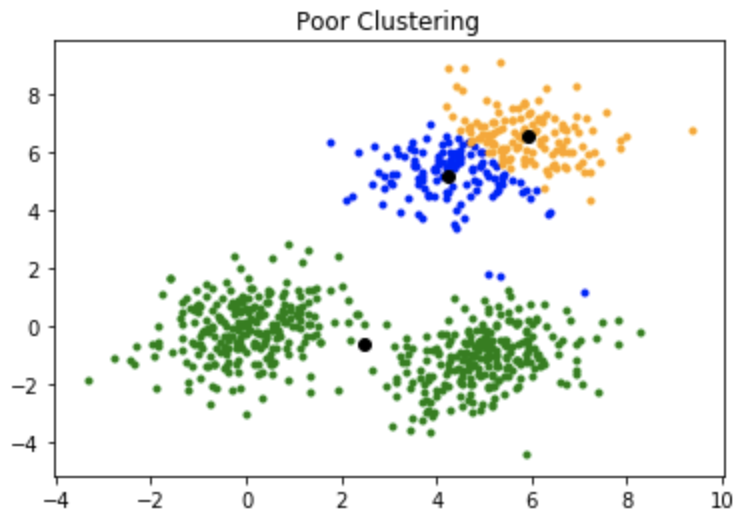In general, the random initialization of kmeans would result in poor clustering similar to the image above The most well known method to solve the problem is to run the algorithm n-times and choose the best resulting clusters, by comparing
the variance inside each cluster. It is assumed that the lesser variance clusters have the better is the actual clustering result.
Second known technique to solve this problem is k-means++. The only difference between k-means++ and standart kmeans is the specially
crafted initialization phase. The steps of k-means++ initialization algorithm are as follows.
Step 1 pick a random datapoint as our first centroid
Step 2 for each point computer distance between the point and the nearest centroid
Step 3 randomly select a new centroid with weighted probability distributions where each point has a probability proportion of D(x)^2 to be chosen
Step 4 repeat steps 2 and 3 untill the k centroids are already chosen.
After these steps are over, standart kmeans algorithm is utilized to obtain a convergent clustering.
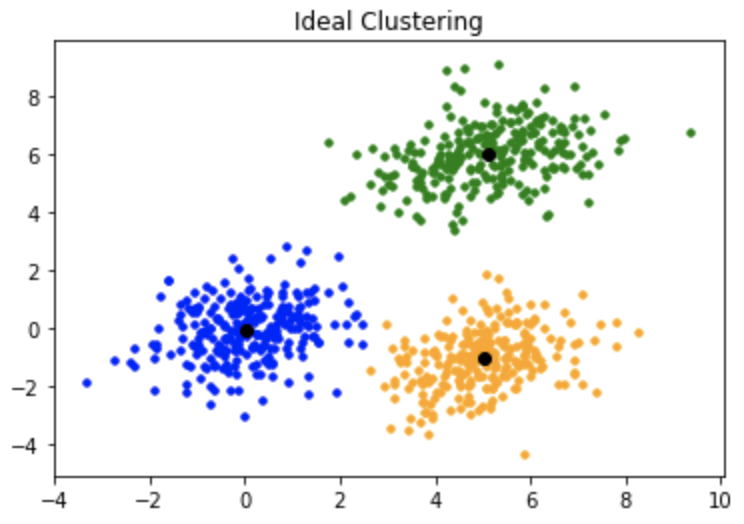The kmeans++ initialization would generally result in better clustering like in the image above.However, this is not the last flaw of the kmeans algorithms. Kmeans also suffers from distance metric inflexibility, meaning that the measure of distance cannot be arbitrary similarity measuer. Secondly kmeans is not robust to outliers as it utilizes mean to obtain the centroids.
To resolve the problem another algorithm was introduced to the game, and k-medoids is its name.
As the algorithm uses medians to calculate the medioids it is more robust to the outliers, also due to the algorithm using dissimilarity measure to estimate the medioids, it is not dependant on distance based measures thus it could be arbitrary dissimilarity measure.
The steps of the algorithm are as follows.
Step 1 kmeans++ initialization
Step 2 associate each datapoint to the closest medioid
Step 3 For each element in cluster, make the element the new centroid, associate each datapoint to the closest medioid and compute the cost.
Step 4 if cost decreased then repeat 2 and 3 else finish.
As you can see the main flaw of the k-medoids algorithm is that it's time complexity is beyond evil, also the k-medoids fails to cluster non-spehrical data points as it uses compactness as clustering criteria not connectivity.
Example code of standard kmeans
from sklearn import cluster, datasets
import matplotlib.pyplot as plt
circle_dataset_x,circle_dataset_y= datasets.make_blobs(n_samples=2000,random_state=170,cluster_std=[1, 2, 1])
kmeans=cluster.KMeans(n_clusters=3,n_init=1,init="random")
result = kmeans.fit_predict(circle_dataset_x)
plt.scatter(circle_dataset_x[:,0],circle_dataset_x[:,1],c=result)
plt.show()
Example of code with repeating kmeans
from sklearn import cluster, datasets
import matplotlib.pyplot as plt
num_inits=1000
circle_dataset_x,circle_dataset_y= datasets.make_blobs(n_samples=2000,random_state=170,cluster_std=[1, 2, 1])
kmeans=cluster.KMeans(n_clusters=3,n_init=num_inits,init="random")
result = kmeans.fit_predict(circle_dataset_x)
plt.scatter(circle_dataset_x[:,0],circle_dataset_x[:,1],c=result)
plt.show()
Example code of standard kmeans with kmeans++ initialization
from sklearn import cluster, datasets
import matplotlib.pyplot as plt
circle_dataset_x,circle_dataset_y= datasets.make_blobs(n_samples=2000,random_state=170,cluster_std=[1, 2, 1])
kmeans=cluster.KMeans(n_clusters=3,n_init=1,init="k-means++")
result = kmeans.fit_predict(circle_dataset_x)
plt.scatter(circle_dataset_x[:,0],circle_dataset_x[:,1],c=result)
plt.show()
Example of code of k-medoids
from sklearn_extra.cluster import KMedoids
import numpy as np
import matplotlib.pyplot as plt
circle_dataset_x,circle_dataset_y= datasets.make_blobs(n_samples=2000,random_state=170,cluster_std=[1, 2, 1])
kmedoids=KMedoids(n_clusters=3,max_iter=1,init="random")
result = kmedoids.fit_predict(circle_dataset_x)
plt.scatter(circle_dataset_x[:,0],circle_dataset_x[:,1],c=result)
plt.show()
The results have shown the k-medioids algorithm in general creates worse clusters than kmeans algorithm and requires a significant number of iterations to get to the same quality of clustering. Although the algorithm is robust to noise and can have arbitrary dissimilarity metric.
Here are examples of of how k-medoids fails with a single iteration and improves after singinificant number of iterations
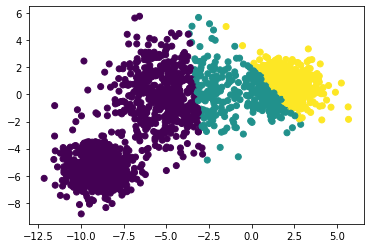</br>Fails after a single iteration 
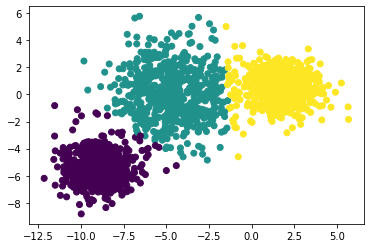</br>improves after hundred iteration